How to Evaluate Measurement Uncertainty
Manufacturing and measurement are closely coupled. An important consideration for the use of measurement results is the associated measurement uncertainty. This article describes common metrology terms and provides an example uncertainty analysis.
Share




“You can’t improve what you don’t measure” is a quote often attributed to Peter Drucker. In the context of manufacturing, we can interpret this to mean that we cannot increase part accuracy, material removal rate or other key performance metrics if we do not measure the outcomes and relate them to processing conditions. Metrology, or the science and application of measurement, is integral to this measure-and-improve sequence.
Metrology is a manufacturing process in the same way as machining, forging or heat treating because it adds value to manufactured components. It is motivated not only by customer requirements for tolerances and surface finishes, but also by confidence in functionality of assembled components.
Regarding assembly, modern combustion engine automobiles have approximately 15,000 parts and large passenger aircraft have millions of parts. For these complicated assemblies to function properly, the part dimensions must conform to design tolerances, surface finishes must meet design requirements and material properties must adhere to design specifications.
We use various transducers to perform measurements in manufacturing environments. Examples include calipers, micrometers, stylus profilometers, CMMs, structured light scanners, rotary encoders and thermocouples.
For each of these measurements, however, there is always uncertainty associated with the outcome. Therefore, when reporting the measurement result for a physical quantity, it is necessary to indicate the reliability of the measurement. We represent this reliability using measurement uncertainty. To explore uncertainty and other metrology fundamentals, let’s begin with definitions of common terms:
- Accuracy (of a measurement): Accuracy is the closeness of the agreement between the result of a measurement and the (true) value. Accuracy is a qualitative concept, so numbers should not be associated with it.
- Error (of measurement): Error is the result of a measurement minus the (true) value. However, we cannot know the true value because every measurement is uncertain. Therefore, in practice a “conventional true value” is sometimes used.
- Uncertainty (of measurement): Uncertainty is a parameter that characterizes the dispersion of values that could reasonably be attributed to the measurement result. Uncertainty can be characterized using statistical methods, such as the standard deviation.
- Resolution: Resolution is the minimum detectable quantity for a selected transducer.
- Repeatability (of results of a measurement): Repeatability is the closeness of agreement between the results of successive measurements of the same parameter carried out under the same conditions of measurement (same procedure, observer, instrument and location over a short time period).
- Reproducibility (of results of a measurement): Reproducibility is the closeness of agreement between the results of measurements of the same parameter carried out under changed conditions of measurement (for example, a new observer or instrument).
Some common misuses of these terms are:
- precision is substituted for accuracy; precision indicates repeatability
- accuracy is used as a quantitative, rather than a qualitative descriptor
- uncertainty is reported for an instrument.
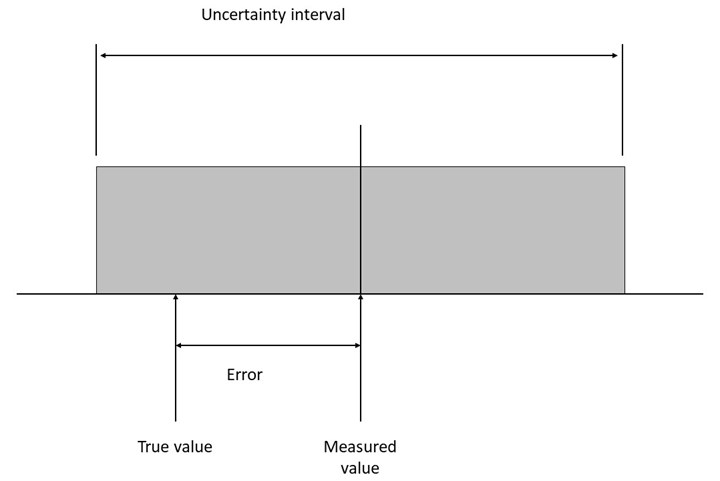
For the final bullet, measurements have an uncertainty, but instruments do not. If the part size or feature changes in measurements performed on a CMM, for example, the uncertainty may vary. Figure 1 describes how these terms are related.
The measured value is the result we obtain from our transducer. It differs from the true value by the error, but we don’t know the true value, so we don’t know the error.
Therefore, we use the uncertainty interval (gray box) to indicate our belief that the true value of the measurement lies within the specified range with a stated level of confidence. This enables the user of our measurement data to make the best decisions about the quantity that it describes.
To evaluate the uncertainty of a measurement, we complete an uncertainty analysis. As an example, let’s consider the density measurement for an aluminum block with nominal dimensions of 10 mm × 12 mm × 50 mm.
As shown in Figure 2, we see that the density (r) measurement, which is the mass (m) of the block divided by its volume (V), is composed of four separate measurements: one mass measurement using a digital scale and three length measurements, a, b and c (that are multiplied to obtain the block’s volume), using digital calipers. Because more than one measurement is required, the density measurement uncertainty is evaluated using the combined standard uncertainty (uc).
We evaluate the combined standard uncertainty for the density measurement using a scary-looking equation; see Equation 1. While Equation 1 may be daunting (it’s called a partial differential equation), its meaning is not.
We see that there are four similar terms which are added together. Each of these terms contains a ratio which represents the sensitivity of density to a particular measurement. The square of this ratio is multiplied by the square of the uncertainty in that measurement.
After we complete this calculation, the value represents one standard deviation of the expected uncertainty for our density measurement. The larger this number, the wider the gray uncertainty interval in Figure 1.
To complete the example, let’s assume we’re using calipers with a digital readout that reports xx.xxx mm, where the right digit indicates the resolution (0.001 mm in this case). For the selected calipers, the manufacturer stated that the length measurement uncertainty is 0.025 mm. We will assume that this uncertainty can be used for each of the three block length measurements.
For the mass measurement, we’ll select a digital scale with a readout of x.x grams (g). The resolution is then 0.1 g. Without other information about the scale, we’ll use our engineering judgement to specify a measurement uncertainty of 0.3 g (three times the resolution). We generally expect the uncertainty to be greater than the resolution.
We used these two transducers to measure the block and obtained the following values: m = 16.1 g, a = 10.142 mm, b = 12.265 mm and c = 50.127 mm. Substitution in Equation 1 gives Equation 2, where we converted grams to kilograms and millimeters to meters.
The result of 48.8 kg/m3 represents one standard deviation from the mean value. For a normal distribution (i.e., a bell-shaped distribution), one standard deviation captures about 68% of all potential density values.
If we examine the four terms that are summed in Equation 2, we see that the first term (2314.82) is much larger than the other three. This first value is associated with the mass measurement using the digital scale. This means that if we desire to reduce the density measurement uncertainty, we should focus our attention on the scale. If reduced uncertainty is required, we could consider investing in a digital scale that offers lower uncertainty for our aluminum block mass measurement.
The result of the density measurement is the mean value ± the uncertainty. The mean value is calculated using the four measured values:
Finally, we express the density measurement result as: 2582.0 ± 48.8 kg/m3. Given this complete measurement description, it is possible to assess whether the block density is acceptable for a particular application.
Related Content
Choosing the Correct Gage Type for Groove Inspection
Grooves play a critical functional role for seal rings and retainer rings, so good gaging practices are a must.
Read MoreProcess Control — Leveraging Machine Shop Connectivity in Real Time
Renishaw Central, the company’s new end-to-end process control software, offers a new methodology for producing families of parts through actionable data.
Read MoreTurning Fixed-Body Plug Gages Inside Out
Fixed-body mechanical plug gages provide fast, high-performance measurement for tight-tolerance holes.
Read More6 Machine Shop Essentials to Stay Competitive
If you want to streamline production and be competitive in the industry, you will need far more than a standard three-axis CNC mill or two-axis CNC lathe and a few measuring tools.
Read MoreRead Next
Setting Up the Building Blocks for a Digital Factory
Woodward Inc. spent over a year developing an API to connect machines to its digital factory. Caron Engineering’s MiConnect has cut most of this process while also granting the shop greater access to machine information.
Read More5 Rules of Thumb for Buying CNC Machine Tools
Use these tips to carefully plan your machine tool purchases and to avoid regretting your decision later.
Read MoreBuilding Out a Foundation for Student Machinists
Autodesk and Haas have teamed up to produce an introductory course for students that covers the basics of CAD, CAM and CNC while providing them with a portfolio part.
Read More















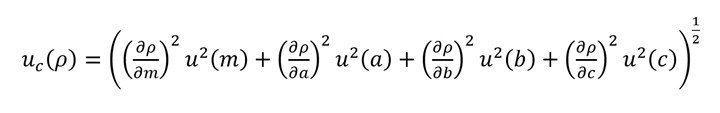
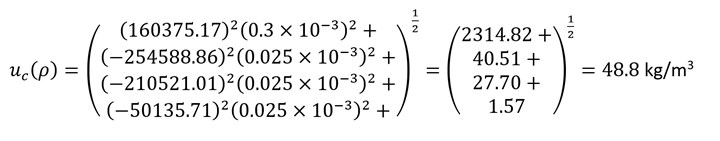

.png;maxWidth=300;quality=90)














