Basic Math For Ballnose Tools
The ballnose end mill is a special sort of tool. Its ability to mill up and down the contours of complex surfaces makes it invaluable to mold shops and other makers of 3D forms. And yet, the tool is lacking in a capability one might take for granted in other cutters: the ability to machine a flat surface.
Share




Takumi USA
Featured Content
View More


ECi Software Solutions, Inc.
Featured Content
View More


Hwacheon Machinery America, Inc.
Featured Content
View MoreThe ballnose end mill is a special sort of tool. Its ability to mill up and down the contours of complex surfaces makes it invaluable to mold shops and other makers of 3D forms. And yet, the tool is lacking in a capability one might take for granted in other cutters: the ability to machine a flat surface.
Because the ballnose tool cuts along a ball instead of a straight profile, it has distinctive characteristics. Its “effective diameter” varies according to the depth of cut. Also, adjacent passes with the tool leave behind scallops on the surface that vary in height according to the stepover distance.
Users can control both of these characteristics by choosing the right parameters for the cut. The nominal diameter of the tool, for example, is the wrong value to use when calculating the correct rpm value to achieve a particular value of surface feet per minute (sfm). The diameter at which the tool cuts is determined instead by how much of the ball is engaged. To calculate this effective diameter, DEFF, use the tool diameter D and the axial depth of cut DOC in the following formula:
Then use this diameter in the rpm calculation. That is:
The important conclusion is this: When using a ballnose tool, the only way to maintain a constant sfm is to change the rpm as the axial depth of cut changes.
The other depth of cut—radial depth, or stepover distance—affects the machined surface. The larger the stepover, the larger the height of the scallops between passes will be. To hold this height below a certain limit, find the right stepover distance using the formula below. Here h is the height of these peaks—in inches, assuming the diameter is in inches—and D is the full diameter of the ball:




























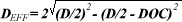




.png;maxWidth=300;quality=90)






